Op-Amps as an Integrator

Introduction

            One of the uses of the op-amps in this lab is to be an integrator of an AC signal. There are several types of signals that could be generated through the function generator. In this lab, we will try to integrate the square, triangle, sine and sawtooth signals and observe the output signal after it is being integrated by the op-amps. What it means by integrated is the mathematical calculation called integral will be done to the signals through the op-amps

Experimental

Before setting up the circuit, some predictions are made concerning the shape of the output as shown below:

The op amps acts as an integrator since:

V_in / R_in = i_C

dq/dt = C dV/dt = i_C

Now in order to have V,

V = 1/(R_inC) * ∫V_in(t)dt

The schematic shown in the picture above did not have an expected result so in order to compensate for it, new values for the components are used as shown in the table below:

Component	Nominal Value	Actual Value
C	47µF	46.6 ± .01µF
Rin	100kΩ	102.7 ± 0.1 kΩ
Rp	100MΩ	9.94 ± .1 MΩ

The setup of the circuit is as follow:

The probe is connected so that red represent the input while blue represent the output. The result of the reading is as follow:

Sawtooth signal

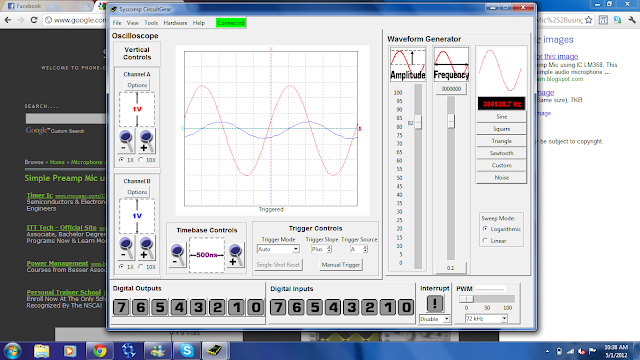sine wave signal

Square wave signal

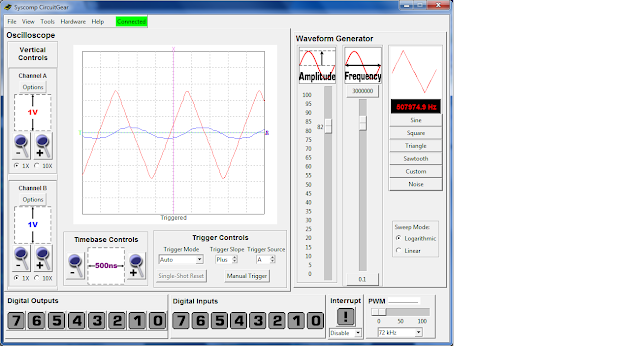Triangle signal

Questions:

1. The 10MΩ parallel resistor is needed so that the capacitor does not saturate the low frequency signal as the resistor will take over and act as a regular op amps instead. A huge resistor is used so that the effect will be apparent when the impedance in the capacitor increased greatly.
2. When integrating a constant voltage, in this case a DV voltage, it will charge the capacitor and it will make the capacitor act as an open circuit which also make all the current goes to the resistor leading to not an integrator but a regular gain op-amps.
3. When the parallel resistor is taken, the capacitor will only integrate the frequency setting it designed to do and will saturate the output when its dealing with low frequency.